Bearing Life Calculation

MONTON Bearing Life

The functions required of MONTON rolling bearings vary according to the bearing application, and these functions must be
performed for a prolonged period. Even if bearings are properly mounted and correctly operated, they will eventually
fail to perform satisfactorily due to an increase in noise and vibration, loss of running accuracy, deterioration of grease, or
fatigue flaking of the rolling surfaces. In the broad sense of the term, bearing life refers to the period during which bearings
continue to operate and satisfy their required functions. Depending on the cause of bearing failure, this bearing life may be defined as:

 • noise life
 • grease life
 • rolling fatigue life

Besides natural deterioration, bearings may fail due to:
 • heat seizure
 • fracture or cracks
 • wear
 • rings becoming scored
 • damaged seals

 If the bearing fails for such reasons, this should not be interpreted as normal bearing life because these failures often occur as a result of selecting the wrong bearings, improper design or manufacture of the bearing surroundings, incorrect mounting, or insufficient maintenance.

Rolling Fatigue Life and Basic Rating Life
When rolling bearings are operated under load, the raceways of their inner and outer rings and rolling elements are subjected to repeated cyclic stress. The rolling contact surfaces of the raceways and rolling elements experience metal fatigue, and scaly particles may separate from the bearing material in a phenomenon called “flaking”. Rolling fatigue life is represented by the total number of revolutions at which the bearing surface will start flaking due to stress. Rolling fatigue life is often also called “bearing life” when the term is used in a more narrow sense.

Even for seemingly identical bearings of the same type, size, and material that receive the same heat treatment and other
processing, the rolling fatigue life varies greatly, even under identical operating conditions. This is because the flaking of
materials due to fatigue is subject to many other variables.
Consequently, the concept of “basic rating life”, in which rolling fatigue life is treated as a statistical phenomenon, is used in preference to actual rolling fatigue life.

Suppose a number of bearings of the same type are operated individually under the same conditions. After a certain period, 10% of them will fail as a result of flaking caused by rolling fatigue. The total number of revolutions at this point is defined as the basic rating life. If the speed is constant, the basic rating life is often expressed by the total number of operating hours completed when 10% of the bearings become inoperable due to flaking.

In determining bearing life, basic rating life is often the only factor considered. However, other factors must also be taken into account. For example, it is possible to approximate the grease life of bearings prelubricated with grease. Since noise life and abrasion life are determined according to individual standards for different applications, specific values for noise or abrasion life have to be determined empirically.

Basic Dynamic Load Rating

The basic dynamic load rating applies to bearings with stationary outer rings and rotating inner rings. It is defined as the constant load that the bearing can endure for a rating life of one million revolutions (106 rev). For radial bearings, the basic dynamic load is given as a central radial load in a constant direction and magnitude, while the basic dynamic load rating of thrust bearings is given as an axial load of constant magnitude in the same direction as the central axis. The basic dynamic load ratings are listed in the bearing tables under Cr for radial bearings and Ca for thrust bearings.

The basic dynamic load rating of multi-row bearing arrangements can be calculated using the following formula: 

for ball bearings: Cj = j 0.7 × C1

for roller bearings: Cj = j 7/9 × C1

 j : Number of rows ( j ≧ 2) 

C1 : Basic dynamic load rating for single-row bearings 

Cj : Basic dynamic load rating for multi-row bearings (where j is the number of rows)

Special care must be taken when calculating the basic dynamic load rating Ca for thrust bearings, as j refers to the number of rows sustaining axial load only. For example, only two rows sustain the a xial load in a four-row DBB arrangement; thus j = 2.

Basic Rating Life

The following relationships exist between basic dynamic load rating, dynamic equivalent load, and basic rating life:

for ball bearings:

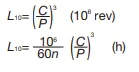
for roller bearings:

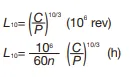
P : Dynamic equivalent load (N) 

C : Basic dynamic load rating (N) 

n : Rotational speed (min⁻¹)

For bearings that run at a constant speed, it is convenient to express the fatigue life in terms of hours.

Life of High-Speed Bearings

When bearings are operated at high speed, the effect of centrifugal force acting on the rolling elements must be considered. In the basic rating life equation on page 190, a ratio of basic dynamic load rating and external load was used, and the internal load generated by centrifugal force was not taken into account.

Note: Bearing life as mentioned above indicates rolling fatigue life, which does not include bearing failure caused by seizure, wear, or the like. It is difficult to calculate how long a bearing will perform until a bearing failure takes place. Please refer to page 190 for details on the definition of bearing life.

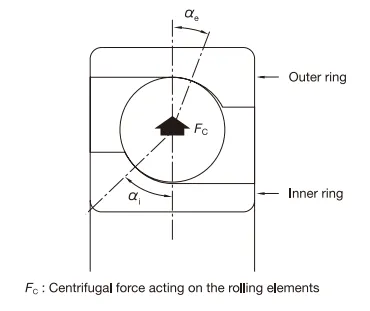
Life of Ceramic Hybrid Bearings

As ceramic balls have a lower density than steel balls, the increase in internal load due to centrifugal force in high-speed
operation is less than with steel balls. Thus, the life calculation will show a longer life.

Life Calculation for Multiple Bearings as a Group
When multiple rolling bearings are used in one machine, the fatigue life of individual bearings can be determined if the load acting on individual bearings is known. In general however, the machine becomes inoperative if a bearing in any part fails. It may therefore be necessary in certain cases to know the fatigue life of a group of bearings used in one machine.

The fatigue life of bearings varies greatly, and our fatigue life calculation equation L10 = ( C/P) p (where p=3 for ball bearings and p = 10/3 for roller bearings) applies to the 90% life, or “basic rating life”. This refers to either the number of revolutions or hours that 90% of bearings of the same type operated under the same conditions can reach.

In other words, the calculated fatigue life for one bearing has a probability of 90%. Since the endurance probability of a group of multiple bearings for a certain period is a product of the endurance probability of individual bearings for the same period, the basic rating life of a group of multiple bearings is not determined solely from the shortest basic rating life among the individual bearings. In fact, the group life is much shorter than the life of the bearing with the shortest fatigue life. 

 Defining the basic rating life of individual bearings as L₁, L₂, L₃ ... and the basic rating life of the entire group of bearings as L, the relationship may be expressed by the following equation:

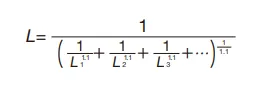
Welcome contact with MONTON for more caculation infomation.